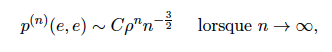1864

Les groupes Fuchsiens forment une classe importante de groupes hyperboliques de type fini. Récemment des progrès significatifs ont été fait dans la théorie des marches aléatoires sur ces groupes – notamment avec un théorème central limite [3, 2, 11] et un théroème local limite [9, 7]. Ces percées ont stimulé d’importantes recherches en théorie des probabilités sur ces groupes mais de nombreuses questions fondamentales restent toutefois encore ouvertes.

Dans ce projet nous allons nous concentrer sur deux de ces questions :

(1) Le théorème local limite donne l’équivalent suivant pour la probabilité de retour en l’originie d’une marche aléatoire :

où C est une constante et p < 1 est le rayon spectral de la marche. Le rayon spectral est l’une des constantes numériques parmi les plus importantes associées à la marche aléatoire. Néanmoins à ce jour il n’existe aucune formule explicite pour dans le cas de groupes hyperboliques non élémentaires et avec un seul bout. Un des buts de notre projet est de développer de nouvelles techniques pour approximer le rayon spectral, afin d’améliorer les dernières bornes connues.

(2) Nous voulons également étudier la question de la géométrie à grande échelle des excursions faites par la marche. Plus précisément, nous voulons montrer que les grandes excursions, une fois renormalisées convenablement, convergent vers l’arbre Brownien continu d’Aldous.

Participants

Sebastian Müller (Aix-Marseille Université)
James Parkinson (University of Sydney)
Bruno Schapira (Aix-Marseille Université)

Sponsor